Quantum Computing Demo at the Computer History Museum
The CHM is a block away from Google headquarters. I took the opportunity today to attend the demonstration of the first commercial quantum computer. The computer, designed by a collaborating network of scientists from several countries under leadership from Dr. Geordie Rose, was built by D-Wave and features 16 qubits or quantum bits. The hardware for a quantum computer (QC) can be one of the following: assemblies of individual atoms trapped by lasers; optical circuits, for example using photonic crystals; semiconductor-based designs, usually including atomic-scale control of dopant atom distribution or quantum dots; and superconducting electronics. Dr. Rose chooses superconducting electronics as the basis of this computer since the fabrication is a known and it scales well. The qubits themselves are not atomic sized but macroscopic features as they use a property of superconducting materials named Cooper pairs. Cooper pairs are bosons, which have no restrictions into how many can occupy a given quantum state. Thus as long as there are no pair-breaking effects, such as temperature or magnetic fields, the paired state has lower energy. At sufficiently low temperature and high pair density, the pairs may form a Bose-Einstein condensate. It is this last property that allows for qubits larger than atomic sized structures, something that makes fabrication and commercialization straightforward with existing technology. But it is also the “sufficiently low temperature” constraint that has this computer operating at 5 mK, very close to absolute zero and about 550 times cooler than interstellar space.
So what do you do with 16 qubits? In 1936, mathematician Alan Turing addressed the problem of computability. His thesis was that all computers were equivalent, and could all be simulated by each other. By extension, a problem was either computable or not, regardless of what computer it was run on. This led to the concept of the Universal Turing Machine, an idealized model of a computer to which all computers are equivalent. However, Turing’s work, and conventional computer science, are only valid if a computer obeys the rules of Newtonian physics. Information (and computation) can never exist in the abstract. Information is always tied to the physical material where it’s stored, what is possible to compute is completely determined by the rules of physics. For example, many important numerical problems reduce to computing a unitary transformation U on a finite dimensional space, a general description of something like, a discrete Fourier transform for example. As it turns out crafting reversible n qubit quantum gates, which are not unlike classical reversible logical gates - well except for the engineering challenge of keeping them coherent at their connection points - provides a way to build a circuit which can carry out such transformations by using an n-qubit state for the input and measuring the transformed qubit state at the output. Sounds easy, well it’s not really, fundamentally there’s no way to setup the input qubits or to read the output qubits without affecting the result. This is where engineering a system that prepares inputs and samples results statistically is necessary, and this is what changes the speedup over a classical computer. Take for example Grover’s algorithm, whereas searching an unsorted database is a linear problem or O(N) the use of a quantum computer and Grover’s algorithm brings this down to O(N^1/2) or what is called a quadratic speedup. This operation is equivalent to inverting a function and it can be used to search exhaustively over a set of possible solutions to solve NP-complete problems. In other words it can speedup significantly any of these.
Lawrence, a colleague from Google took pictures of most of the slides at the presentation. Here’s also a link to dwave. So why is not IBM or Intel doing this? Good question read here for a take on that.

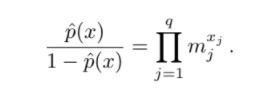
Comments